流体のシミュレーションについて

紹介記事

流体力学

擬スペクトル法

皆さんは、流体という言葉を聞いて、どのようなものを想像するでしょうか？水や空気、あるいはそれらの流れを思い浮かべる方が多いと思います。多分大体あっています。流体力学は、そのような「決まった形を持たないもの」の動きを扱う学問です。気象予報や気候予測などには、流体力学の知見が欠かせません。空気や海水の流れが天気や気候に影響するからです。

ところで、その流体の動きをシミュレートするといっても、あまりイメージのわかない人もいるかもしれません。今回の記事を通して、そのイメージが少し明確になれば嬉しく思います。

とりあえず眺めてみよう

これは、「ケルヴィン・ヘルムホルツ不安定性（Kelvin-Helmholtz instability、以下KH不安定性）」と呼ばれる現象をシミュレートしたものです。流体内で大きな速度差がある時に、わずかに揺らぎを与えると、速度差のある境目に波が立ちます。

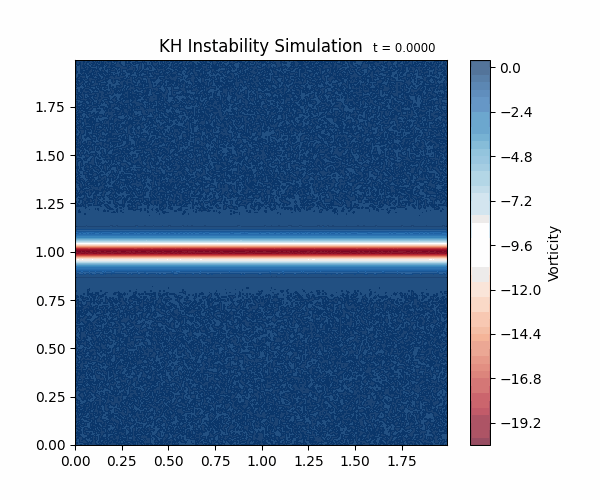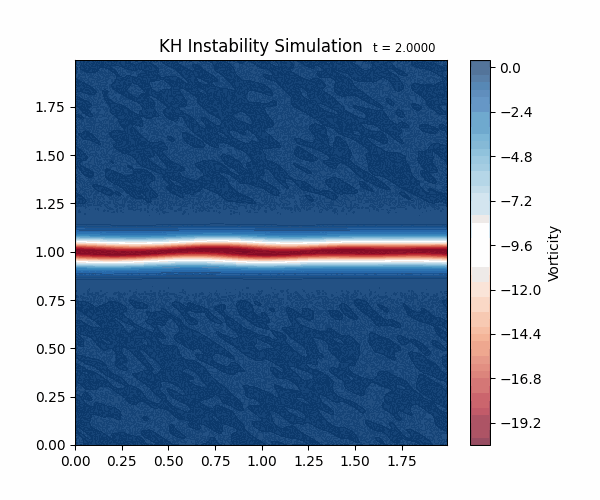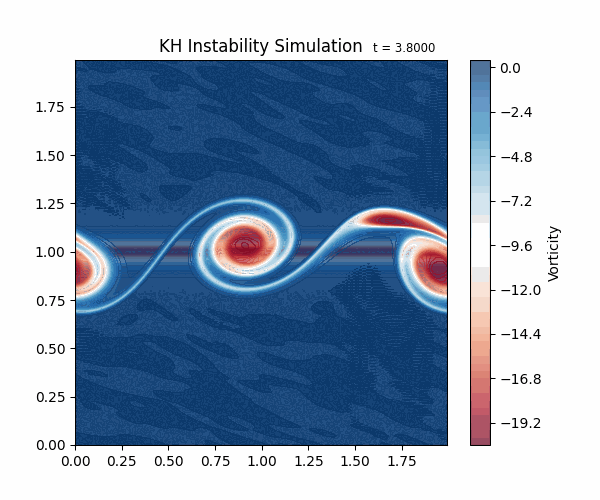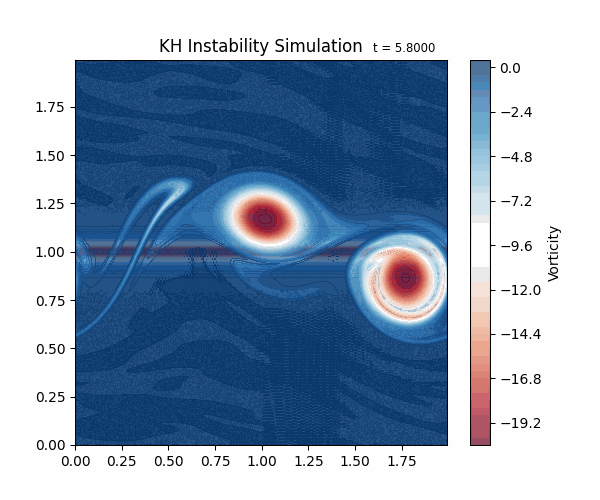
Gravitational Lens Simulation — 図1: シミュレーション結果（初期状態の残像が残ってしまっていることに注意）

これは実際の自然界でも条件がそろえば発生する現象です。例えば、雲の上に風が吹くと、雲の表面に波のような模様ができることがあります。これは、雲の中の水滴や氷晶が、風によって揺らされてできたものです（図2）。

Clouds with Kelvin-Helmholtz instability — 図2: KH不安定性を示す雲の例（credit: GRAHAMUK at the English-language Wikipedia）

流体力学の定式化

流体力学シミュレーションでは、ただ闇雲に計算しているわけではありません。物理法則に裏打ちされていなければなりません。通常、流体力学では下のナヴィエ・ストークス方程式（Navier-Stokes equation、NS方程式）を用います。ある地点での流体の速度 \(\boldsymbol{u}\) が時刻 \(t\) に従ってどのように動くのかを定式化したものです。

\[ \frac{\partial \boldsymbol{u}}{\partial t} + \boldsymbol{u} \cdot \nabla \boldsymbol{u} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \boldsymbol{u} \]

ここで、\(\rho\) は流体の密度、\(p\) は圧力、\(\nu\) は粘性（動粘性係数）を表します。この式自体は、「こんなものあるんだ」程度で構いません。この式を「なんとかして」コンピュータで扱える形にし、数値計算を行なっているわけです。

このNS方程式も含め、物理法則の多くは、微分方程式で表現されます。なんだかよくわからないですが、実際には少しだけ時間が経ったときに、位置や速さなど、注目している量がどのように変化するかを表しているに過ぎません。^[1]よって、実際にシミュレーションするときも、時間を少しだけ進めて、注目したい量の変化を計算し、それを繰り返し、合算することで、最終的な値を求めていきます。

原理的には、この操作は手計算でできます。しかし、多くの場合あまりにも時間がかかり過ぎます。リチャードソンという人が、1920年に手計算で気象予報を試みましたが、6時間後の気象予報に1ヶ月もかかってしまったそうです^[2]。よって、現代的な数値シミュレーションのほとんどはコンピュータを用いて行われます。

今回用いた数値計算手法

今回は、「渦度法」と「擬スペクトル法」と「1次精度オイラー法」という手法を用いています。渦度法は、流体の運動を渦度という量で表現する方法です。渦度とは、流体の回転の強さを表す量で、流体の運動をより簡単に扱うことができます。擬スペクトル法は、流体の運動をフーリエ級数展開（何？でかまいません）して表現する方法です。これにより、シミュレーションを実行するプログラミングコードの記述が非常に簡単になります。

付録：実際に作成したプログラム

ここでは、実際に作成したプログラムを紹介します（可視化の方法が少し違うため、図1の見栄えとは多少異なる）。PythonのJupyter Notebookのローカル環境で実行しました。環境によってはもしかしたら動かないかもしれないので、ご了承ください^[3]。

ところで、手軽にPythonを始めたい人は、Google Colaboratoryを使うと良いです。Googleが提供しているJupyter Notebook環境で、Pythonのコードを簡単に実行できます。Google アカウントがあれば、すぐに使えます。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc

# --- パラメータ設定 ---
Nx, Ny = 256, 256
Lx, Ly = 2.0, 2.0
dt = 0.0002
nu = 1e-4
steps = 30000

# --- 通し番号と画像を保存する配列 ---

i = 0
ims = []

# --- グリッド生成 ---
x = np.linspace(0, Lx, Nx, endpoint=False)
y = np.linspace(0, Ly, Ny, endpoint=False)
X, Y = np.meshgrid(x, y)

# --- 波数ベクトル ---
kx = 2 * np.pi * np.fft.fftfreq(Nx, d=Lx/Nx)
ky = 2 * np.pi * np.fft.fftfreq(Ny, d=Ly/Ny)
KX, KY = np.meshgrid(kx, ky)
K2 = KX**2 + KY**2
K2[0, 0] = 1e-10

# --- 初期条件 ---
U0 = 1.0
delta = 0.05
vorticity = -(U0 / delta) * (1 / np.cosh((Y - Ly/2) / delta))**2

mode_x = 2
disturbance = .02 * np.random.randn(Ny, Nx)
vorticity += disturbance
# vorticity += 0.2 * np.sin(2 * np.pi * mode_x * X/Lx)

omega_hat = np.fft.fft2(vorticity)

# --- アニメーション準備 ---
fig, ax = plt.subplots(figsize=(6, 5))
im = ax.imshow(vorticity, extent=[0, Lx, 0, Ly], origin='lower',
               cmap='RdBu', animated=True)
cbar = plt.colorbar(im, ax=ax)
cbar.set_label("Vorticity")
title = ax.set_title("KH Instability Simulation")
time_text = ax.text(0.8, 1.02, f"t = {0:.4f}", fontsize="small", transform=ax.transAxes)
ims = [[im, time_text]]

# --- メインループ ---
for i in range(1, steps):

     # ψ の計算
    psi_hat = - omega_hat / K2

    #u_hat, v_hat の計算

    u_hat = 1j * KY * psi_hat
    v_hat = 1j * KX * psi_hat

    #dwdx_hat, dwdy_hat の計算
    dwdx_hat = 1j * KX * omega_hat
    dwdy_hat = 1j * KY * omega_hat

    u = -np.real(np.fft.ifft2(u_hat))
    v = np.real(np.fft.ifft2(v_hat))
    dwdx = np.real(np.fft.ifft2(dwdx_hat))
    dwdy = np.real(np.fft.ifft2(dwdy_hat))

    nonlinear = u * dwdx + v * dwdy
    nonlinear_hat = np.fft.fft2(nonlinear)
    

    omega_hat += dt * (-nu * K2 * omega_hat - nonlinear_hat)

    # 描画更新
    if (i % 1000 == 0 or i == 0) and (i < steps):
        # Euler更新
        omega = np.real(np.fft.ifft2(omega_hat))
        im = ax.imshow(omega, extent=[0, Lx, 0, Ly], origin='lower',
                       cmap='RdBu', animated=True)
        time_text = ax.text(0.8, 1.02, f"t = {i*dt:.4f}", fontsize="small", transform=ax.transAxes)
        ims.append([im, time_text])

    i += 1

# --- アニメーション作成 ---
anim = animation.ArtistAnimation(fig, ims, interval=150, blit=True)

rc("animation", html="jshtml")
plt.close()
anim.save("./plot4.gif",writer='imagemagick') # gif で保存
anim

巽友正. 流体力学. (1982). 培風館.
2021年度東大理学部物理学科アクティブマター班. (2021). 流体モデルのシミュレーション. https://event.phys.s.u-tokyo.ac.jp/physlab2021/articles/zj1e8jlry75q/